Caches Deep Dive - Part 1: The Basics
Introduction to caches
Disclaimer: Opinions shared in this, and all my posts are mine, and mine alone. They do not reflect the views of my employer(s), and are not investment advice.
The idea of locality:
Like many other ideas in computer architecture, the idea of caches originated from two common patterns in which a processor requests data from a memory:
Temporal locality: This is a pattern where the same memory location is being accessed repeatedly
Spatial locality: Here, memory locations close to each other are accessed within a short time frame
One of the most common manifestation of these patterns is in loops. For example, this is a code snippet to find the sum of all elements in a matrix:
int matrix[100][100];
int sum = 0;
for (int i = 0; i < 100; i++) {
for (int j = 0; j < 100; j++) {
sum += matrix[i][j];
}
}This example demonstrates both patterns of locality:
Temporal: The memory location occupied by variables sum, i, and j are all accessed repeatedly to execute this loop
Spatial: Each element of matrix[100][100] occupy adjacent memory locations - the loop counters (i and j) change predictably, and access these nearby locations
If you look at most programs, such patterns are very common (although loops are only a few lines of code, they usually take the longest to execute since they have to be repeated). This pattern is also true for the memory that stored instructions to be read - except in case of branches, the processor always reads instructions one after the other - i.e. spatial locality is exercised here.
The idea of locality tells us that often, a processor either accesses the same memory location, or accesses nearby memory locations - so if data from these locations can be fetched faster, it will reduce the overall execution time. This was the motivation behind caches.
What is a cache?
In very simple terms, a cache is a fast memory that sits between the processor and a slow memory. For this definition to make sense, two questions need to be answered:
What makes a memory fast?
Type of RAM: A Random Access Memory (RAM) is the fundamental structure - an arrangement of transistors - that can store data bits. Broadly, there are two types - Static RAM (SRAM), and Dynamic RAM (DRAM). SRAMs are faster, but need more transistors. DRAMs are slower, but use fewer transistors. Caches always use SRAM cells.
Search time and design complexity: The way any memory works is: it takes an address as input, compares the address with all its locations, and sends out the data when a matching address is found. So if the memory is larger, it makes it harder to search. Microarchitecturally speaking, this manifests in one of 2 ways:
Slower clock
More pipeline stages
Either way, the latency (time between requesting a memory data, and actually receiving it) increases. Caches are smaller memories, which ensure they have lower latency - they either operate with higher clock frequency, or they have fewer pipeline stages. Hence, caches are fast memories
(For more details, check out my earlier post on CPU pipelining-,Why%20pipelining%3F,-All%20digital%20systems), where I talk about the how every logic stage needs a minimum clock period, and if this cannot be met, we need to add pipeline stages. The same logic applies in memory design)
Proximity to the processor: When the floorplan of a chip is made, the cache is always placed close to the processor. So the amount of wires between the cache and processor is reduced, which reduces the signal propagation time.
Why do we need a slow memory (called main memory) in the first place?
Everything that makes a cache fast comes from a compromise - to maintain sufficient memory capacity
SRAM cells need more transistors, so they consume more area than DRAM
Cache needs to be small to reduce latency. So if all memory were cache, then that would reduce the latency.
Chip floorplans are usually very congested - so placing a huge memory close to the processor may not be possible (main memory is an off-chip memory)
Essentially, if we want a sufficiently large memory, that is also fast - the idea of caching helps. Caches provide high speed memory access to the most frequently used locations, and the slow main memory provides larger memory capacity for cheap - so the processor can enjoy the best of both worlds.
How does cache utilize locality:
Based on the current description of the cache, the benefits of temporal locality is obvious - if the same memory location is being accessed repeatedly, then that memory location can be moved to the cache, so that each access is fast.
To understand how cache uses spatial locality, its important to understand the structure of a typical cache. There are few keywords:
Word: It is the size of the unit of data that the processor reads from the cache in a single cycle
Cache Line: It is the entity (multiple words) that the cache fetches its main memory and stores together. All the words within a line are always together.
Tag: A unique ID that is used to map a memory address from the processor to the cache line.
Cache Block: Cache line + Tag (sometime this is also called Cache line)
This is an example of a cache with 2 lines, each having four 32 Byte words:
Cache lines have words from adjacent memory locations. So if a processor wants to read two locations adjacent to each other within a short time span, it is likely that both the words are in the same cache line. However, if the processor is reading two locations that are far apart, two different cache lines will need to be fetched. This is how caches benefit from spatial locality.
Steps within a typical cache access:
Before going further, I want to quickly share how a processor works with the memory hierarchy.
The processor executes a set of instructions. This processor has a word size of 1 Byte. Let’s say the current instruction needs to access 4 Byte of data, starting from memory address = 1000.
If the access is a Read:
The processor sends a request to the cache, which indicates that it wants to read data from memory address = 1000 to 1003 (since Word size = 1 Byte, each address location maps to 1 Byte)
The cache checks if the requested memory addresses are already present in any of its cache lines:
If YES, then the cache returns the data for the requested addresses (This is called a Cache Hit)
If NO (This is called a Cache Miss),
Cache requests the cache line(s) containing the address 1000 to 1003 from the main memory. (It is possible that these addresses are in 2 or more different cache lines - each would need a separate request)
The main memory returns the requested cache line to the cache.
The cache needs to decide where the cache line will be stored (Either store it in an empty space, or get rid of some existing data). If existing cache line has to be removed, it is called Cache Line Eviction.
Once the cache line is stored, the cache can return data for the requested addresses to the processor
Once the processor receives data from the cache, it can continue its execution.
If the access is a Write:
The processor sends a write request to the cache, indicating writes to memory address = 1000 to 1003. The processor also sends the corresponding write data
The cache checks if the requested memory addresses are already present in any of its cache lines. There are two schemes of write that the cache can follow after this step:
Write-Through scheme: Here, every write from the processor to cache, is also propagated to the next levels in the memory hierarchy (If there is only one cache, then the data is written to the cache, and also the main memory). If this scheme is followed:
If it is a Cache Hit, then the Word(s) in the existing Cache Line (or multiple cache lines) is replaced with new data. The cache line is then written back to the main memory.
If it is a Cache Miss, the the data is directly written to the main memory without allocating a new cache line. This approach is called Write-Around.
Write-Back scheme: Here, write data from the processor is only updated in the cache. Other caches, and main memory is only updated if needed - this typically happens when the cache line needs to be evicted from the cache (Eviction can happen during a future read/write). If this scheme is followed:
If it is a Cache Hit, update the word(s) in the cache line(s). No other memory is updated
If it is a Cache Miss, then the required cache line is first fetched from the main memory into the cache. To do this:
The cache checks if it has an empty cache line, or if it needs to evict a cache line
If a cache line needs to be evicted:
Check if this cache line was modified by a previous write. If Yes, first write the cache line to main memory. Then evict the cache line.
If the cache line was not modified before, directly evict the cache line
After fetching the cache line(s) for corresponding addresses, update the word(s) in the cache line. Again, no other memory is updated until it is necessary.
Although the Write-Through scheme has a simpler cache logic, it has some disadvantages:
Writing data from cache to main memory adds latency, which makes the overall write operation slower
Usually, the additional latency can be masked (by starting the next memory operation in parallel with the write back to main memory). However, the bigger problem is the additional power consumption due to the extra writes to main memory.
Write-Back has the potential to reduce this additional latency and power-consumption - but this comes at the cost of increased cache complexity (which could make the cache slower). Some modern caches also have the ability to switch between both schemes based on the workload.
This is a time-chart that represents the different steps when a processor sends a read request, which results in a cache miss, and the cache lines that needs to be evicted was written earlier using the Write-Back scheme:
This is just an overview of reads and writes in caches. Additional complexity gets added as we look at other features in this and future posts.
Mapping memory addresses to cache lines
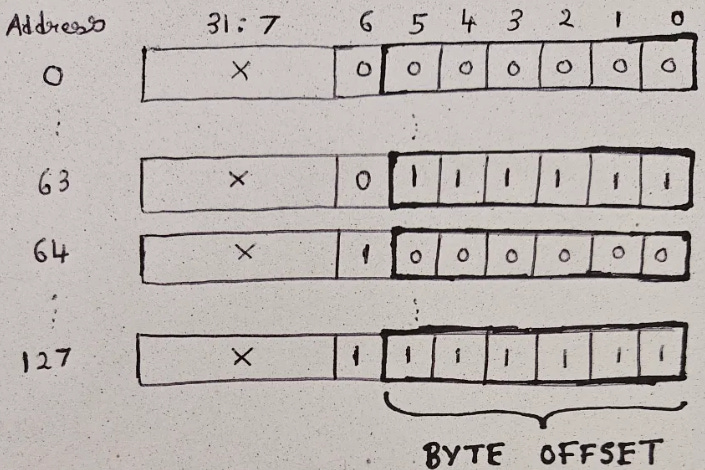
I’ll explain memory mapping with an example. Consider a system with 32-bit memory addresses. We want a 64 KB cache for this system. Each cache line can hold 64 Byte data (this is just the words, it does not include tag). Assume that the word size is 1 Byte.
How to map memory addresses to entries of this cache?
Each cache line holds 64B. which is 64 Words. To utilize spatial locality, adjacent addresses will be stored in the same line. For example, address 0 to address 63 belong to the same cache line, address 64 to 127 are in the same line, and so on… If you represent these addresses in binary, the rightmost (LSB) 6 bits toggle within each cache line - hence, the address bits [5:0] represent the Byte Offset.
Now that we have dedicated bits to access each word in a cache line, the next step is to map different addresses to different cache lines. As the cache size is 64KB, and each cache line is 64B - so we have a total of 64KB/64B = 1024 cache lines.
To map each contiguous 64B chunk of data in memory to a cache line, there are different approaches, each with its pros and cons:
Simple bit mapping
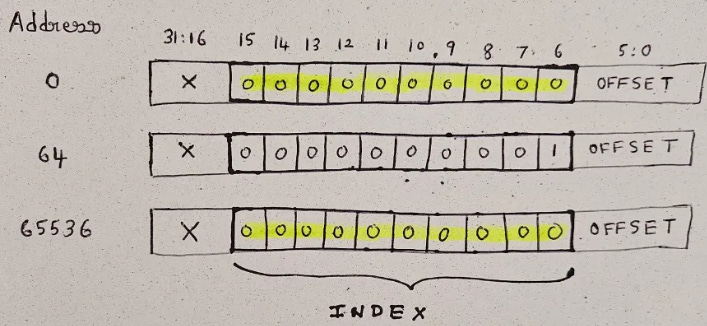
The simplest approach is to pick the 10 bits after byte offset (address bits [15:6]), and use them to map each 32 bit address to one cache line. This set of bits is called the Index.
For example, address = 0 maps to cache line = 0, address = 64 maps to cache line = 1, and so on…
However, the problem with this method can be seen after the first 1024 64B chunks are assigned.
For example, when you look at the bits of address = 65536, you will see that the Index = 0, which is same as address = 0. This means that the cache cannot differentiate memory requests from the processor for address = 0 and address = 65536. This phenomenon is called Aliasing.
To overcome this issue, we introduce the idea of tag in the next approach.
Direct mapped cache
Direct mapped cache is just a small addendum to the simple bit mapping method - after assigning the offset and index, the remaining bits (address bits [31:16] in our example) as set as the Tag and stored along with the cache line.
Two cache lines having the same index will still map to the same cache line. However, the tag bits are then compared to differentiate between the two memory addresses - this way, aliasing can be avoided.
While Direct mapped caches work well in theory, and are used in a lot of simple memory hierarchies. However, their mapping is fixed - which often results in very low cache utilization. In our example above, if we have a processor that is repeatedly accessing memory address = 0, followed by memory address = 65536, then each time, the same cache line gets used - so only one of the two addresses can be stored at the cache at once. However, all the other 1023 cache lines are empty - if the mapping allowed for it, we could have easily used another cache line so that both the memory addresses can be accessed directly through the cache, which makes the memory operations much faster. The next approach to mapping allows this.
Fully Associative cache
Fully associative cache enables maximum utilization of the cache - by allowing all any address to be stored in any cache line. Achieving this is simple - just get rid of the fixed index and generate indices on the fly.
In our example, if the cache were fully associative, then aside from address bits [5:0] (which continue to be the offset), all other address bits ([31:6]) are stored as the tag. This way, when a new cache line needs to be stored, the cache just allocates any empty location, and saves the corresponding tag. When the processor requests a memory location, the tag from every cache line is compared with address bits [31:6] for the request address in order to find the matching cache line.
The microarchitectural implementation of such a cache is done using Content Addressable Memories (CAMs), as shown in this diagram:
This is a simplified implementation for a cache system with 2 lines. Here, we need 2 CAM cells that can hold any tag values. For our example, let’s say the cache already has 2 lines occupies with Tag1 = 100 and Tag2 = 200. If the processor requests a memory address with Tag = 200, then the following happens:
The comparators read Tag1 (=100) and Tag2 (=200) from the CAM cells, and compare with the input Tag (=200)
The comparators returns 0, and 1 respectively (Tag2 matches with the input Tag)
Since one of the comparators returns 1, the output of the OR operation is 1, indicating that the requested memory address is a cache hit
The encoder is designed in a way to map the 2 bit input to generate a 1 bit index:
10 maps to 0
01 maps to 1
11 is not valid (each Tag is unique), and we don’t care about 00 (as it is a cache miss)
Based on the generated index, the cache line can be picked that corresponds to the requested memory address
While fully associate cache ensures the least possible cache misses in any scenario, their implementation in real systems is usually tricky. As you can see from the microarchitectural diagram, even a 2 cache line system involves a lot of logic. In our example cache, since there are 1024 cache lines, we need 1024 CAM cells, 1024 comparators (each comparing 26 bits), an encoder for 1024 bit, and OR operation for 1024 bits. This makes the cache power hungry and slow, and hence, the fully associative approach is only used in highly memory critical systems.
Set Associative cache
This represents a compromise between direct mapped and fully associative cache. Basically, the cache is divided into sets of cache lines. There is a fixed, direct mapping between memory addresses and the different sets. However, within each set, the mapping is fully associative. This way, we get the best of both worlds.
In out example cache, let’s say we follow a set associative mapping, with 256 sets. This means, that the 1024 line cache is now divided into 256 sets with 4 cache lines each. Now, we have address bits [5:0] as the offset (as usual), and bits [13:6] as the index - we only need 8 bits now as the mapping is to sets (256), not lines (1024). The remaining bits ([31:14] are stored in the cache line as the tag.
Within each set, we have a fully associative mapping using the CAM + comparator structure that I mentioned earlier. This will ensure some flexibility within the set, and the cost of a minimal area and power cost (In our example, that would be 4 CAM cells and comparators). Fully associative caches also provide better utilization - in the scenario I mentioned for direct mapped cache - now, although both address = 0 and address = 65536 map to the same set, then can occupy two different cache lines within the set.
Set associative caches also provide flexibility - by reducing the number of sets, the utilization can be improved (at the cost of area and power, of course). Hence, they are the most common implementations in modern caches.
Cache Replacement Policies:
As mentioned earlier, when a memory request from the processor results in a Cache Miss, if often needs a new cache line to be added to the cache. If the cache is already full (for a fully associative cache), or the index after mapping is occupied, an existing cache line needs to be removed to accommodate the new cache line. The logic behind doing this is called the Cache Replacement/Eviction Policy. These are some typical approaches:
Random replacement
Any random cache line is removed. This is the easiest to implement, but does not utilize any benefits of locality.
First-In, First-Out (FIFO) replacement
Replace the oldest cache line (the one that was added first). To implement this, 1-bit is added to indicate which line is the oldest. When this line is removed, a new line is set as the current oldest line. This policy is better than random replacement, since it is a reasonable assumption that the cache line that was added many cycles earlier may not be needed anymore.
Least Recently Used (LRU) replacement
This is the most optimal policy as it can maximize benefits from temporal locality - since a cache line that is accessed now is likely to be accessed soon, replace the cache line that was least recently accessed. However, implementing a full LRU policy is challenging, since it would need the full timestamp of recent to be stored with the cache line, and all timestamps need to be compared during each eviction to decide which line is least recently used. Hence, simper versions of LRU are usually implemented:
a. Pseudo LRU
With each cache line, store a small counter (typically 3-4 bits). The counter starts at 0
Each time a cache line is accessed, the counter is incremented. If the counter reaches maximum value (=7 for 3-bit counter), do not increment anymore
During eviction, compare the counters, and evict the cache line with the least counter value
Periodically decrement all counters (To ensure that all counters do not saturate over time)
b. not-Most-recently-Used
Here, we set 1 bit to indicate the cache line that is used recently. During eviction, eliminate a random line that in not the most recently used. This is a simple implementation, but is better than random replacement.
Least Frequently Used (LFU) replacement
This is very similar to LRU, but focusses on frequency of accesses (over the last few clock cycles) instead of just the recent access. Implementation is generally complex.
Just like mapping, picking the correct replacement policy is important to ensure high cache utilization. There are more complex policies for replacement that I’m not covering here.
In general, the best cache replacement policy usually depends on the workload. A lot of research happens in this field, which interesting new solutions. For example, simple machine learning algorithms like a perceptron are being used to effectively decide which cache line to evict.
Other bits stored in the cache line:
So far, the cache line has the following elements:
Data (typically multiple words from consecutive addresses)
Tag (A unique ID to map every memory address to a cache line)
In addition to these, there are 2 more important bits that every cache line has:
Valid: It is a single bit for each cache line that indicates if the data stored in the corresponding cache line is valid or not. The cache uses this information in 2 ways:
Check if any cache line is empty (If Valid bit = 0, it means the line is empty)
Evict a cache line (Removing a cache line is same as changing its Valid bit from 1 to 0)
Modified: This bit indicates that the cache line has been modified by a Write using the Write-Back scheme. During eviction, the cache checks this bit to decide if write to main memory is necessary. This bit is not needed if all writes are Write-Through.
Bits needed for cache replacement policy: Based on the type of cache replacement policy.
These bits, along with the cache line’s unique Tag, is together called the Tag Array.
This concludes the basic ideas in cache design. If you want to continue with your cache learning, check-out the next post in this series here:
References:
Majority of the ideas in this post were taken from the book Next-Gen Computer Architecture: Till the End of Silicon, by Prof. Smruti R Sarangi.
The ebook is available for free here - https://www.cse.iitd.ac.in/~srsarangi/advbook/index.html